Ortodroma

Az ortodroma, vagy ortodromikus távolság, a földfelszín két pontja közötti legrövidebb távolsága amit Föld felszínén a két pontot összekötő főkör mentén mérünk. Mivel a gömbi geometria lényegesen eltér az euklideszi geometriától, a távolságszámításra használt matematikai képletek is eltérőek. Az euklideszi geometriában a legrövidebb távolságot a két pontot összekötő egyenes, a nemeuklideszi geometriában a két pontot összekötő geodetikus vonal (gömb esetén főkör) mentén mérjük. Az ortodroma meghatározása a navigáció egyik alapfeladata.

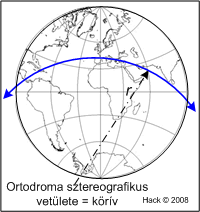
A Mercator-vetületen az ortodroma egy szinuszhullámból levezethető. A képen egy állandó irányú vonal, egy loxodroma is látható.

• 
• 
• 
• 
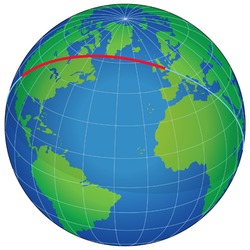  London–Los Angeles

Matematikai leírása

A gömb középpontjában elhelyezett derékszögű koordináta-rendszerben a gömb és az ortodromát kimetsző ${\displaystyle {\vec {n}}(A,B,C)}$ normálvektorú sík egyenlete:

${\displaystyle x^{2}+y^{2}+z^{2}=R^{2}}$

${\displaystyle Ax+By+Cz=0}$

A gömbfelület földrajzi és derékszögű koordinátái közötti kapcsolat:

${\displaystyle x=R\cos \varphi \cos \lambda }$

${\displaystyle y=R\cos \varphi \sin \lambda }$

${\displaystyle z=R\sin \varphi }$

Ezek alapján felírható az ortodroma felületi egyenlete:

${\displaystyle A\cos \lambda +B\sin \lambda +C\tan \varphi =0}$

Ugyancsak a transzformációs formulákból meghatározhatók a két földrajzi pontot kitűző

${\displaystyle {\vec {OU_{1}}},{\vec {OU_{2}}}}$

helyvektorok, és ezekből a normálvektor három koordinátája (vektoriális szorzat).

Források

• Szász Pál: A differenciál- és integrálszámítás elemei. Közművelődési Kiadóvállalat, Budapest, 1951.
• Hajós György: Bevezetés a geometriába. Tankönyvkiadó, Budapest, 1960.